What is a L̶i̶n̶k̶e̶d̶ Skip List?
Nuh-uh, that is not a typo
William Pugh first described skip lists in 1989, so they’re not exactly new. Nevertheless, they are new to me - I came across them a week ago, and went I want to share that with someone! For lack of a more Gen-Z analogy, think of this as me coming across a nice video on Instagram and sharing it with you.
Since this is not an academic undertaking and I’m simply writing it because I find skip lists cool - we’ll talk about intuition, not implementation.
Linked Lists
Good ol’ Linked Lists! They’re made up of nodes and each node points to the next node.
We always have to traverse a Linked List in a straight line, going from one node to another.
Can we search faster than O(n) in Linked Lists?
Not really, but let’s think for bit.
What if our Linked List is always sorted? Still no way out. Since each node points to only the next node, you have to traverse linearly come what may.
We now know two things:
We have a rule - the Linked Lists we’re talking about are always sorted
Each node in a linked list points only to its neighbour, this is a general property of Linked Lists
Weird Idea
What if we could make a node point to multiple forward nodes? For example, in the diagram above - we make [3] point to both [6] and [19]. If someone is searching for [21], they start at [3] and check both its forward nodes. Since we know that the list is sorted, we can jump straight to the node [19] and look ahead.
In searching for [21], we skipped 5 elements. Now what would be a good name for such a data structure...
Skip Lists
Unlike a Linked List, a skip list has multiple forward nodes and is always supposed to be sorted. Here’s a picture that will do you a world of good:
How would we find [17] here?
We start at [HEAD], looking from the highest forward pointer.
[HEAD]’s highest forward pointer = [6]. Since the list is sorted, [17] will obviously be ahead of [6] - move to [6]
We are at [6]. Start looking from the highest pointer again.
[6]’s highest forward pointer = NIL (consider it infinity). [17] will be behind infinity. Move down.
[6]’s second highest forward pointer = [25]. [17] must be behind [25]. Move down.
[6]’s third highest forward pointer = [9]. [17] must be ahead of [9]. Move to [9].
We are at [9].
[9]’s highest forward pointer = [17] Found it!
This is how [17] was inserted to form the skip list in the diagram above. The exact same process as searching for it.
Three Questions
Q: You get a sense that the time complexity of skip lists would be less than linear since they are skipping over elements. But what is the exact asymptotic complexity?
A: It is logarithmic. Refer to the original paper.
Q: You can see that the number of forward pointers for each node seems completely random. How is it decided?
A: A coin flip. I am not kidding. You can read the original paper (again)
Q: Where are skip lists even used?
A: Skip lists are an alternative to self-balancing data structures like B-Trees. The most famous use case of B-Trees - databases. You can Google around to find well-known database companies using skip lists for some form of in-memory storage.
Buh-bye
Your head’s probably buzzing with unanswered questions, and they should. If you have a tiny bit of intuition about what skip lists are and how they make operations like search and insert faster, that’s my job done.
Remember - blog posts are nuggets of knowledge, be wary of treating them like reservoirs. If you want depth, books and papers are the way to go.
Resources
Want to dive deeper? Read the original paper.
Acknowledgement
All skip list illustrations are borrowed from the original paper.


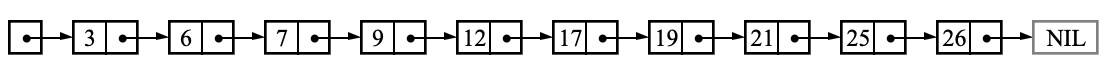


Insightful I must say.