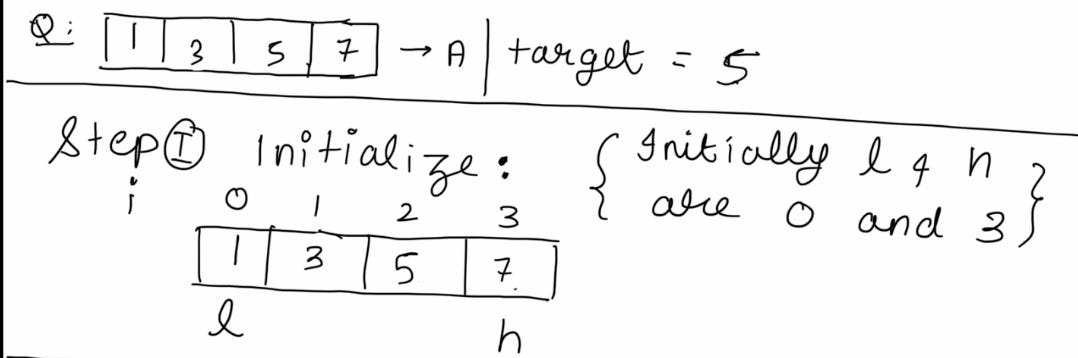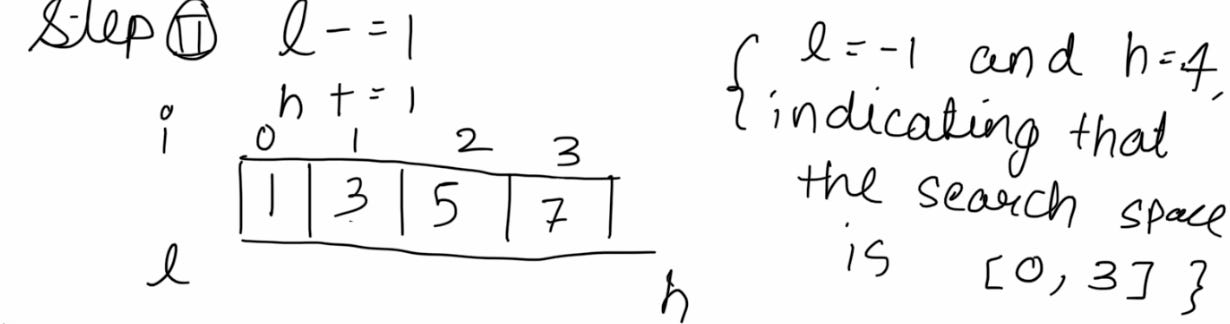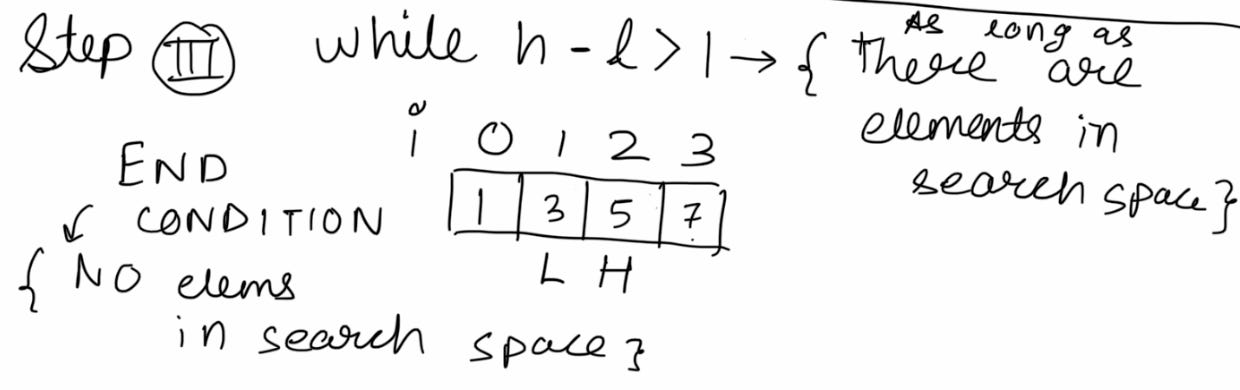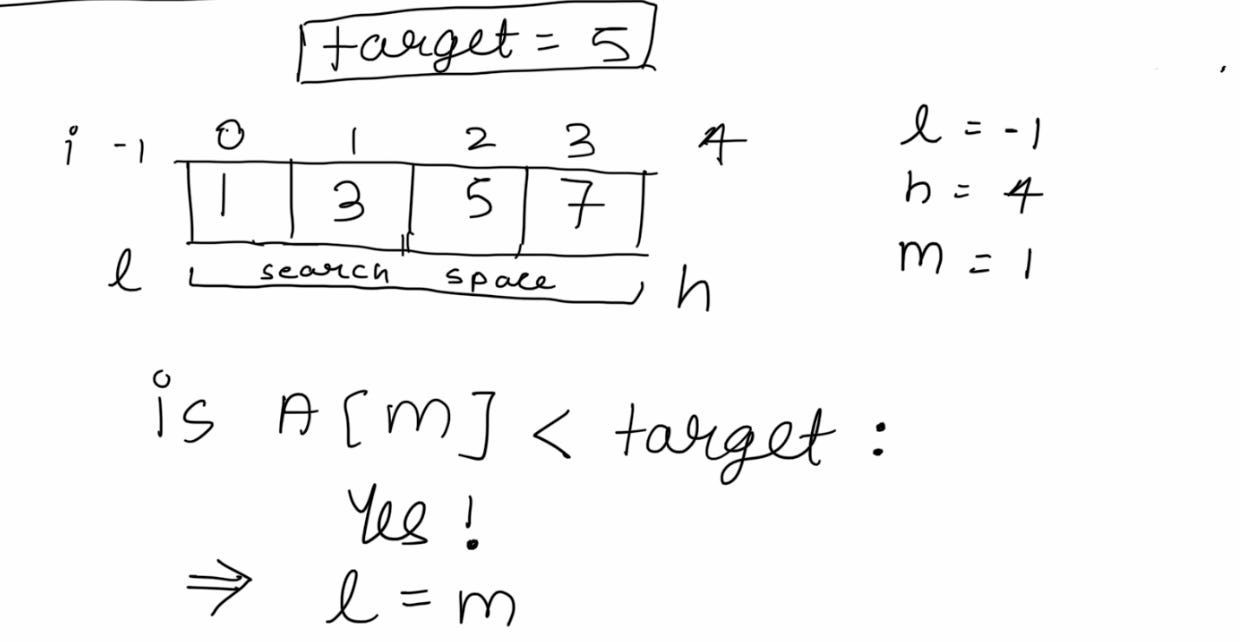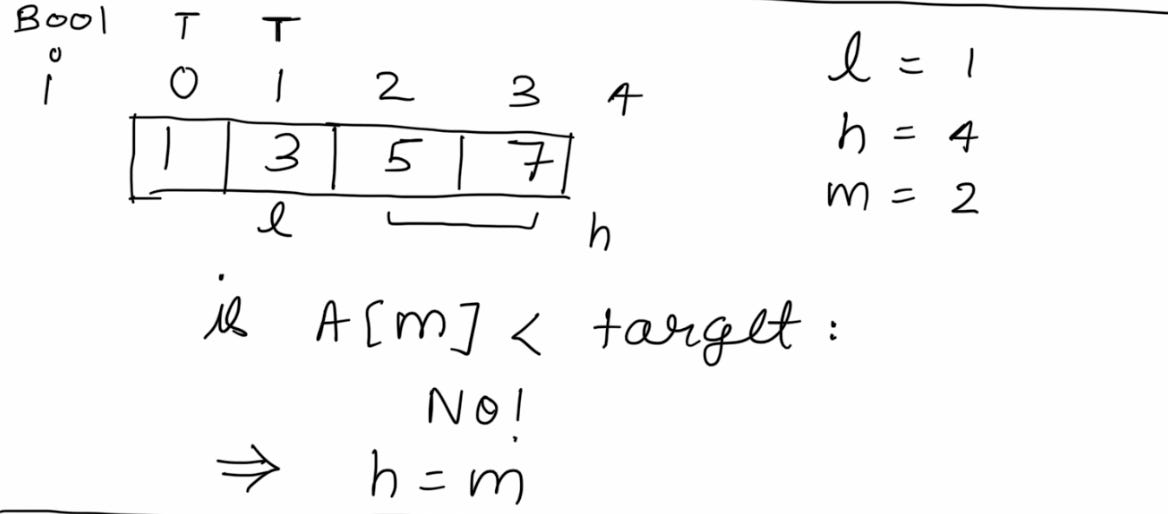Yet Another Binary Search Tutorial

Let's try and change the way you think about Binary Search.

Blog posts are mighty unreliable? Agreed. Take a leap of faith with this one, even though I know that’s what they all say.

There is only one thing that I ask of you.

Read and re-read it as many times as it takes to comprehend it entirely.

Why read this?

If you are reading this, you probably know what Binary Search is. Why then, should you spend your precious time reading this?

Having spent a fair bit of time solving and re-solving Binary Search problems, I faced the following issues repeatedly:

• Lack of a template: You know what Binary Search is, but you don’t have a set template to implement it, leading to mysterious errors each time you re-solve questions eg. indices going out of bounds or infinite loops.

• Your template doesn’t generalize well: Ok, your tuition teacher gave you a fancy-schmancy template which you ate up like candy. It seems to work for all the problems he taught, of course ;) Trouble starts when you come across a new problem and just can’t figure out how it fits this template.

• Applying Binary Search to a weird problem: Binary search was supposed to be about sorted numbers in lists, right? How do I even apply it to this freaking weird problem which doesn’t have anything sorted?!

Open up any Youtube video talking about Binary Search and there are guaranteed to be hundreds of comments asking very implementation-specific questions like: “Why does your left bound move to mid + 1 instead of mid?”

Read this and you will not struggle to implement Binary Search ever again.

Pre-Requisite

The only pre-requisite is an extremely elementary comprehension of what Binary Search is.

What if you know nothing? That’s cool too, since your mind is a blank canvas. Just do this bit: watch/read through any resource on Binary Search, and understand it enough to answer the following questions:

1. In your own words, what is Binary Search?

2. Why is the time complexity of Binary Search log(n)

If you want something spoon-fed, this video does a good job of explaining the idea behind Binary Search. It shows only a recursive implementation, this GeeksForGeeks article will show you an iterative implementation as well.

The principle

Now comes the most pertinent question, how do we rewire our brain to think about Binary Search?

Read this very carefully:

1. Assume you have an array of Boolean values only

2. This array always follows a pattern: it always has ‘n’ true values (where 0 <= n <= length of array) and the remaining are false.

3. Your job is to find the first false value.

Doesn’t make sense? Don’t worry. Just read it a couple of times, try to understand what you can and move ahead.

An Example

Let’s solve the most basic Binary Search problem using our principle:

Find a number ‘x’ in a given sorted array ‘A’:

A = [1, 2, 3, 4, 5, 6] ; x = 4

Following the 3 steps listed in our ‘The Principle’ section.

1. We need an array of Boolean values only. Let’s convert this to a Boolean array. How? For each value, ask a ‘question’ and note down the answer to the question.

2. For example, let’s ask the question: ‘Is the number less than 4?’ to each number in the array A = [1, 2, 3, 4, 5, 6]. Using this, we get the boolean array A = [T, T, T, F, F, F]

3. We can clearly see the first false here is on index 3 (0-indexed). Which is our answer!

Another Example

Let’s pick up a slightly tougher example to drive the point home. Note that the elements are not even sorted.

Consider the following Leetcode question (understand what is asked very carefully before proceeding):

Let us consider Example 3. Following our three step process.

1. We need an array of Boolean values only. How do we convert this to a Boolean array? Once again - for each value, ask a ‘question’ and note down the answer to the question. This gives us our Boolean array.

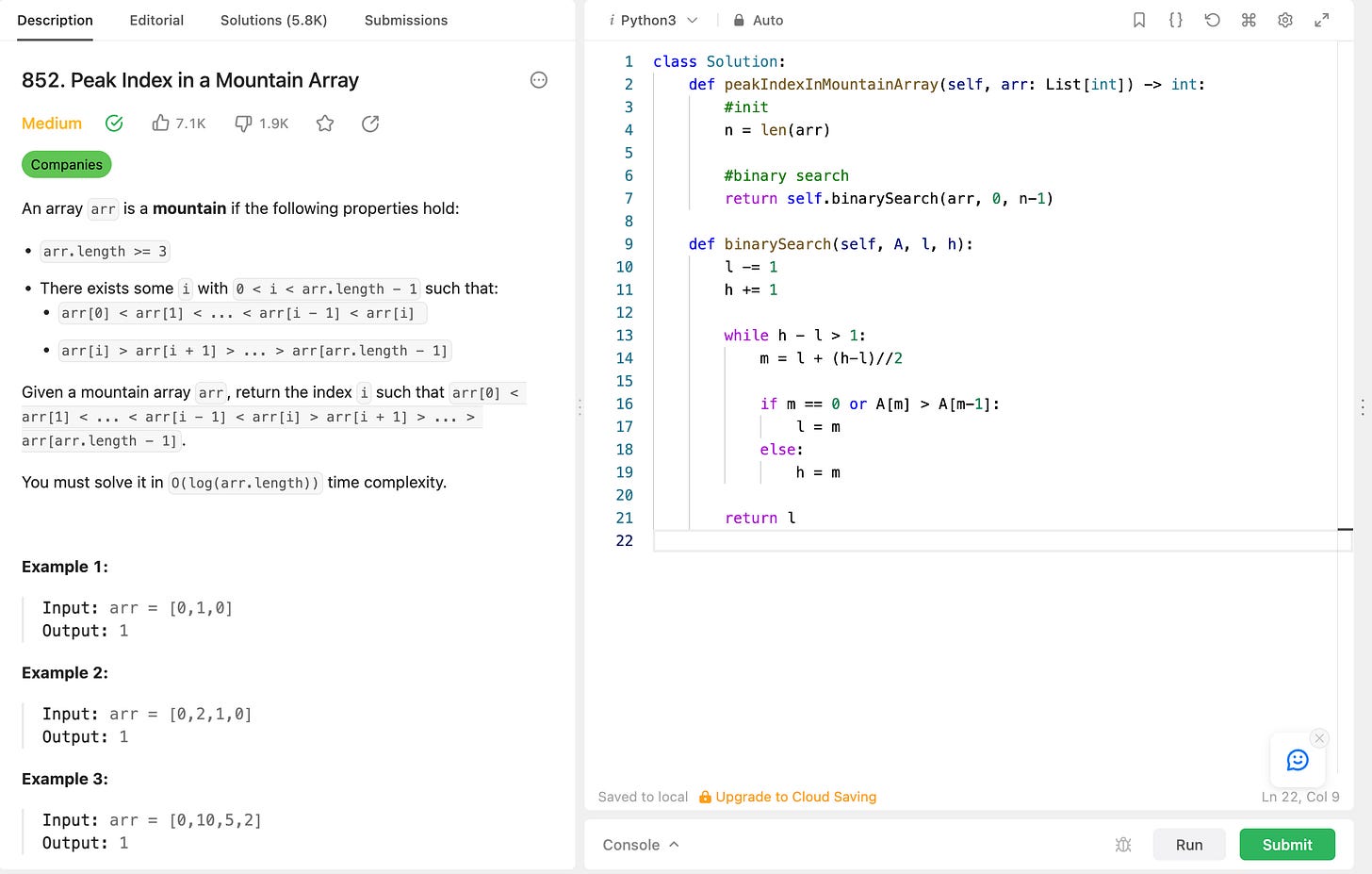
2. What question should we ask? Since we want the peak element, let’s try: Is the element greater than its previous element? Using this, our array A = [0, 10, 5, 2] gets converted into A = [T, T, F, F]. Note that since the 0th index can never be the peak, its value will always be true. We can slightly modify our question to: Is the element greater than its previous element OR is it the first element in the list?

3. We see that the first false here is index 2 → is it the answer? No! But we can see that the first false always gives us the index after the peak. Thus the peak index is 2 - 1 = 1 which is our answer!

Principle revisited

Having seen two examples, I want to revisit our foundational principle and pen down some thoughts on it.

1. The 3-step principle is the basis of Binary Search. We want to ask a question such that our array gets converted into a Boolean array of the form True(s) followed by False. Why? Since we know we want to find the first false, we can safely discard half of the search space on each iteration (If we get a true, go right to find the first false, if we get a false, look left for any other false before it).

2. Like in our second example, we might need the last true value instead of the first false. Doesn’t matter! We know the first true will always be behind the first false.

3. The ‘question’ we ask to convert our array into a Boolean array is, in mathematical terms, a function (you input numbers and get back Boolean values). Your only job in solving Binary Search problems is to find the right question to ask.

Skeleton

Now for the fun part, lets put it into practice.

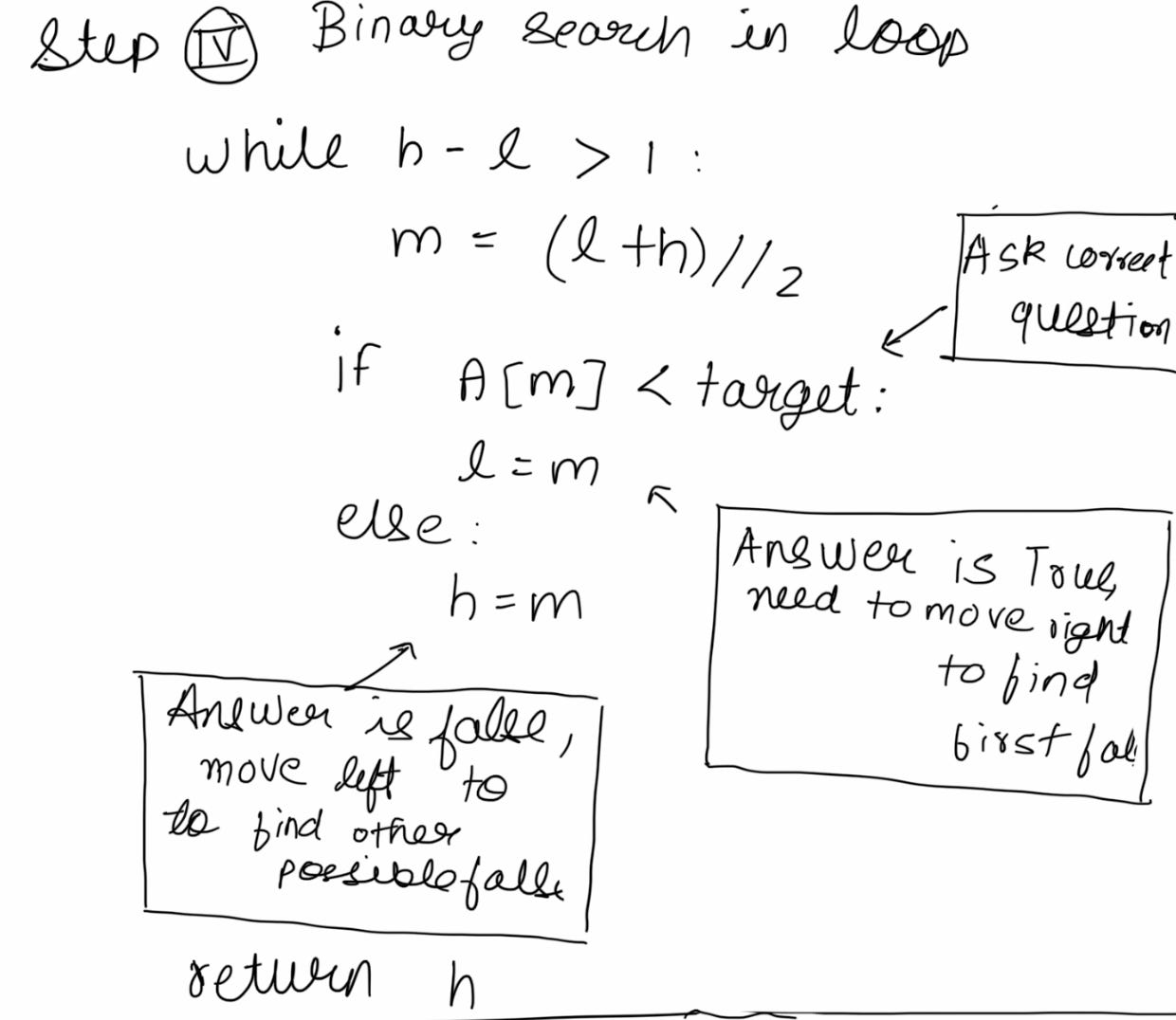
Lo behold, this is our Binary Search template! Let’s take a look at each step.

Taking the example of finding 5 in the array A = [1, 3, 5, 7]

• We initialize with a call to the function, passing low(l) and high(h) as 0 and len(array)-1 respectively

  

• We manipulate low and high such that the indices between low and high are our search space

  

• We continue our Binary Search as long as there are elements in the search space, a typical end condition would look like this

  

• We modify our low and high depending on the QUESTION ASKED, it is very important to ask the right question such that we get true(s) followed by a number of false values.

Dry Run

A dry run with our example:

• Initially, we have the entire array as our search space. A[m] = 3

• Notice the Boolean values on the top and how our search space has shrunk into half.

  

• Search space no longer exists, meaning we have completed our Binary Search.

Edge Cases

• The element might not exist in the array:

  • If A = [1, 3, 5, 7] and target = 4, then our Boolean Array will be [T, T, F, F]

  • The first false gives us index 2 and A[2] = 5

  • Hence it is always important to check if the index returned contains the element or not

• Depending on the question asked, the array might be all false or all true values, it is important to check these border conditions

  • If A = [1, 3, 5, 7] and target = -1 then our Boolean Array will be [F, F, F, F]

  • The first false value is index 0 and index[0] = 1

  • If A = [1, 3, 5, 7] and target = 9 then our Boolean Array will be [T, T, T, T]

  • The first false value is index 4 and A[m] does not exist

• Depending on the question asked, you might require the last true value as your answer instead of the first false value (read the examples below to understand)

Solved Examples

Here are a few Leetcode questions solved using this template. Be sure to pay attention to:

• The question asked

• The value returned after Binary Search (low or high)

• How edge cases are handled

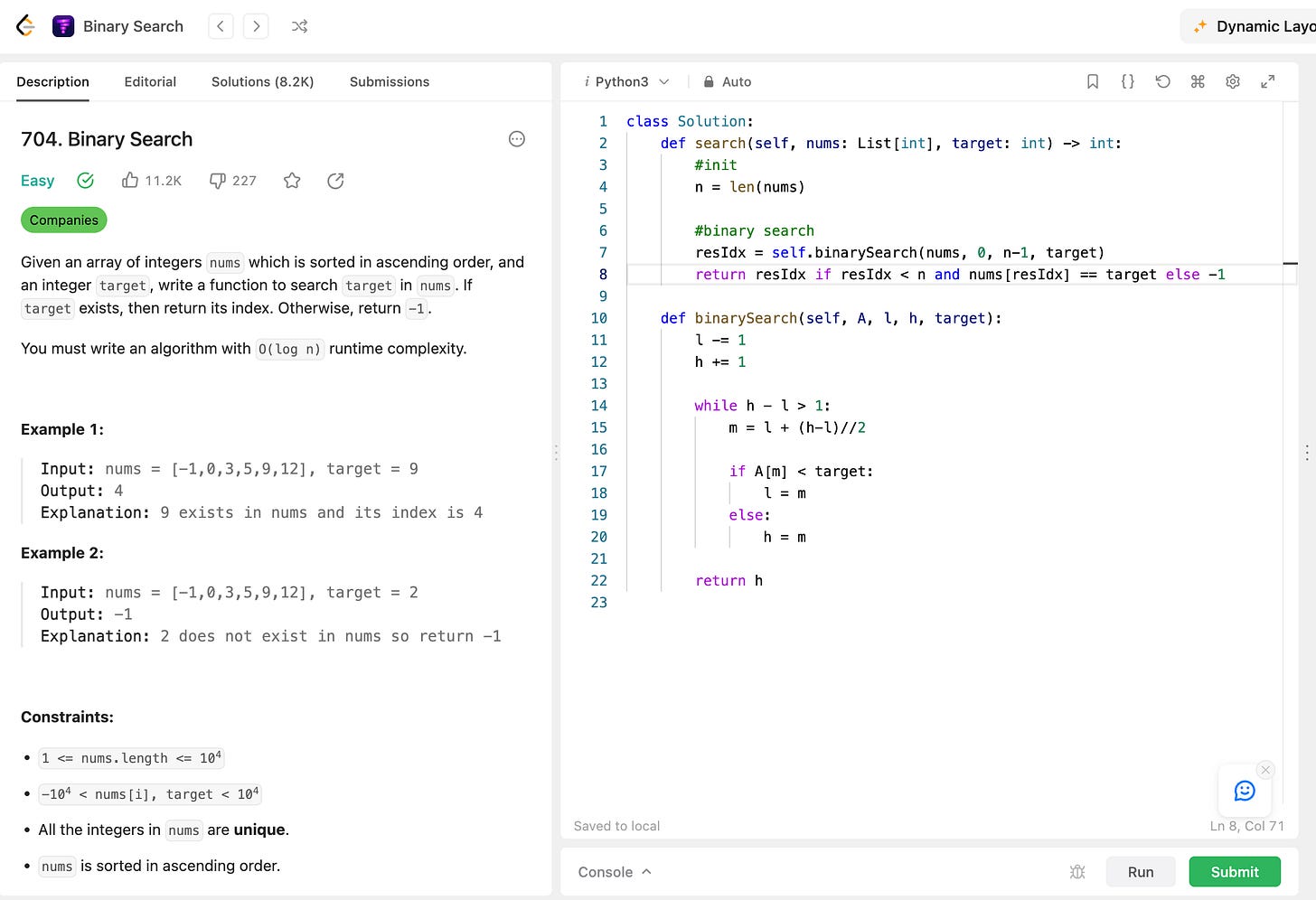
1. Classic Binary Search

2. Peak Index in Mountain Array (note that the elements are not even sorted)

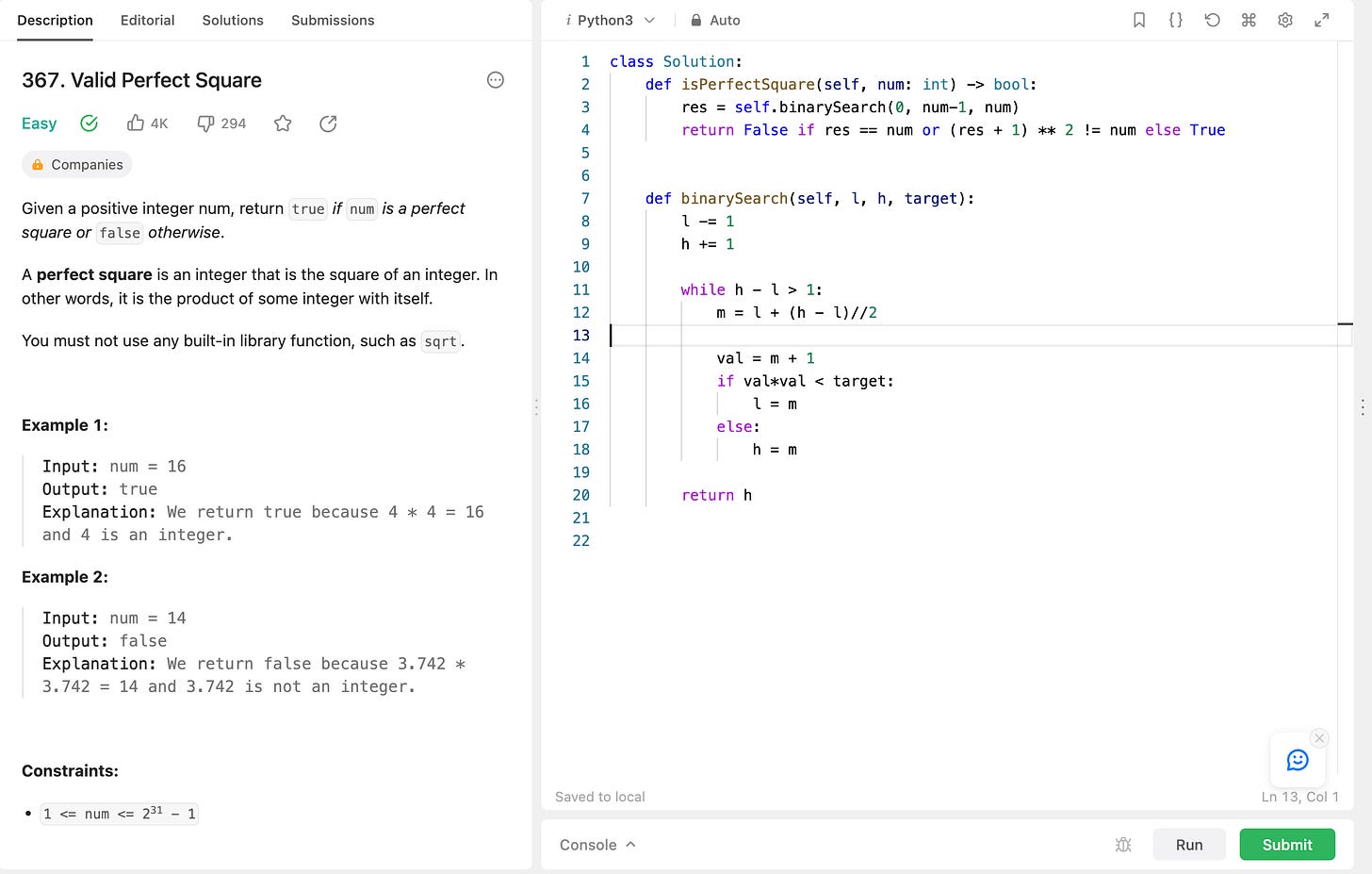
3. Valid Perfect Square

What to do next

1. Firstly, understand the template and why it does what it does. Grab a pen and paper and try working it out. Read and re-read this article until you do.

2. After this, the easiest way to ingrain this into your veins would be to grab a pen and paper and solve questions you already know the solution to using this template.

3. Finally, to see how well it generalizes, solve new questions using this template.

Even if you did not understand a word of what I wrote, I would strongly encourage you to check out the Codeforces article attached in the resources below. It a tad more mathematical but there’s a chance things might make sense after reading it.

Resources

• Codeforces article that is the inspiration behind this piece

• List of Binary Search problems to try - I have first-hand solved ALL of them using the template above

Feel free to ping me if you want solutions or any further explanations :)