Yet another Minimum Spanning Tree Tutorial - Prim's Algorithm
Nothing fancy, just expect to be able to talk about + solve questions on Minimum Spanning Trees using Prim's Algorithm
Blog posts suck. If you want to really, really know something, please pick up a book.
That said, books are dense. Books are expensive. Some books are badly written, even.
Think of this as a quick-and-dirty alternative OR a loving nudge to go and read some academic text.
Why read this?
You want to read this blog post if:
You are one of those lazy ones (not a personal attack) who reach out for blog posts over books
You know nothing about Minimum Spanning Trees, but you do understand what graphs are
You want to be able to solve questions on Minimum Spanning Trees
The worst thing blogs do is leave out a critical piece of information and not tell you about it - I solemnly swear not to stoop that low. Anything that I skim over will be acknowledged loudly so that you can look it up.
Pre-Requisites
Just a high-level understanding of what graphs are.
What’s a Minimum Spanning Tree?
No more than 10 points, I promise.
The concept of an MST(Minimum Spanning Tree) applies only to weighted graphs i.e. graphs where every edge has a particular weight.
No book-jargon. Let’s look at a question to understand what MST’s are:
Read the question and the answer carefully, until you feel you have understood what is being asked
The only two important features of the solution path are:
There exist no cycles
It includes all the points
Can you draw any other paths which satisfy these conditions? (Hint: Many exist)
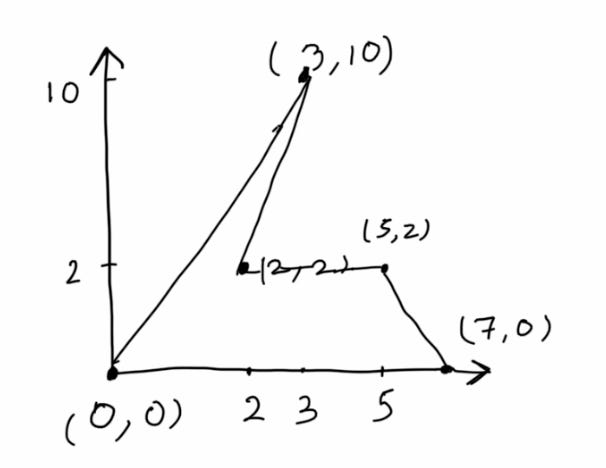
Exhibit A:Exhibit B:
Note: There is no edge between (0,0) and (7,0) in both diagrams. You might have an alternate path where these two might be connected.
The two paths above are Spanning Trees. Any graph which satisfies the two conditions listed above is a Spanning Tree.
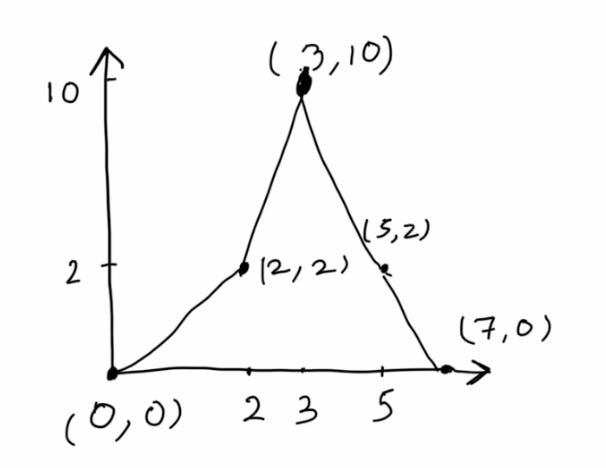
Now for the big reveal. What is a Minimum Spanning Tree? A Spanning Tree where the cost of the path is the least. That’s it! A Minimum Spanning Tree is a path where:
There exist no cycles
It includes all the points
The cost of the paths is the least, out of all such paths that exist
How to construct the Minimum Spanning Tree?
If you aren’t sure what an MST is, go back to the previous section and re-read it. If you still aren’t, it’s okay - people don’t always get it straight away. Continue reading.
There are two main algorithms used to construct the MST for a graph: Prim’s Algorithm and Kruskal’s Algorithm.
Let us start with the first one.
Prim’s Algorithm
In minimum words:
Bring all nodes into the MST by picking the minimum cost edge from all edges seen so far
Ignore the edge if a cycle is formed.
Focus on the key terms: See, pick, ignore.
It may not make much sense right now, but hold tight.
Dry Run
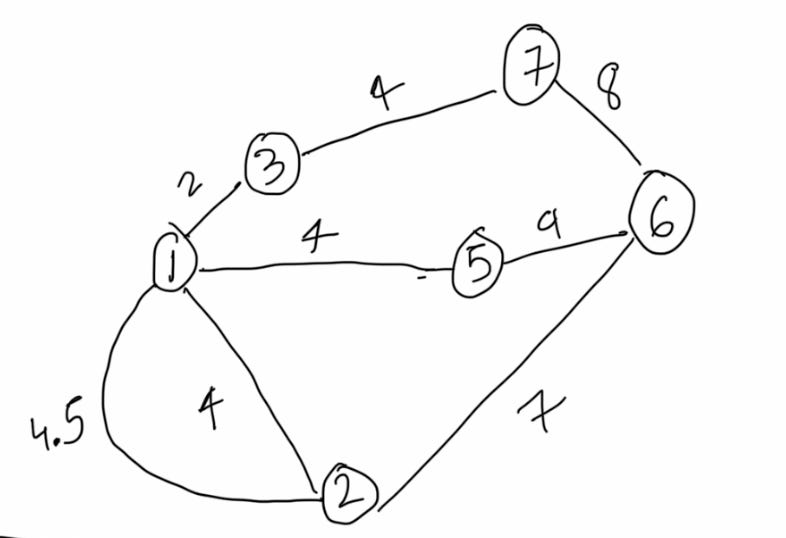
We will construct the MST for this ugly graph.
Since no node is in the MST, let’s pick any arbitrary node.
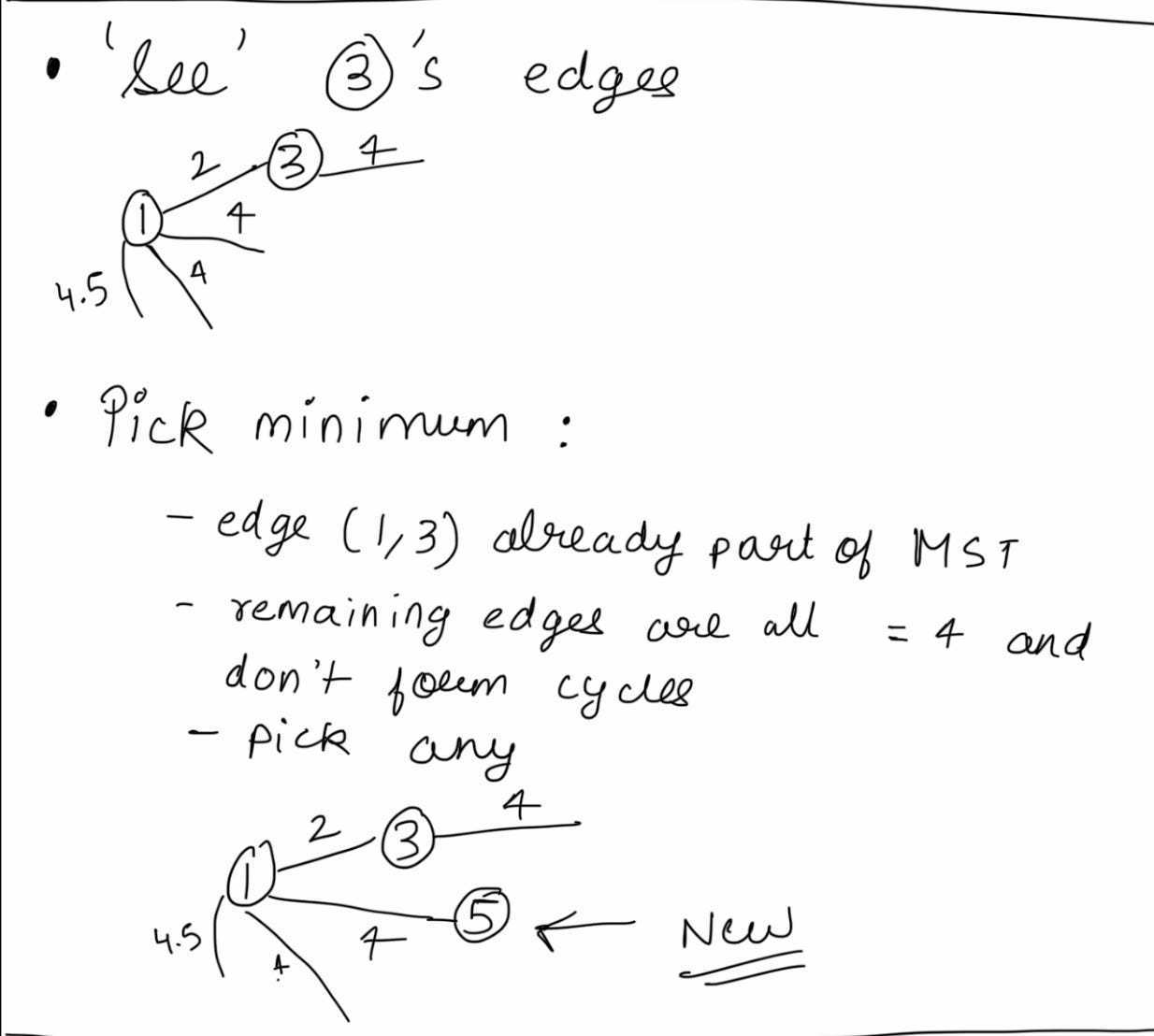
See, pick and ignore, remember? Let’s try it for the next node.
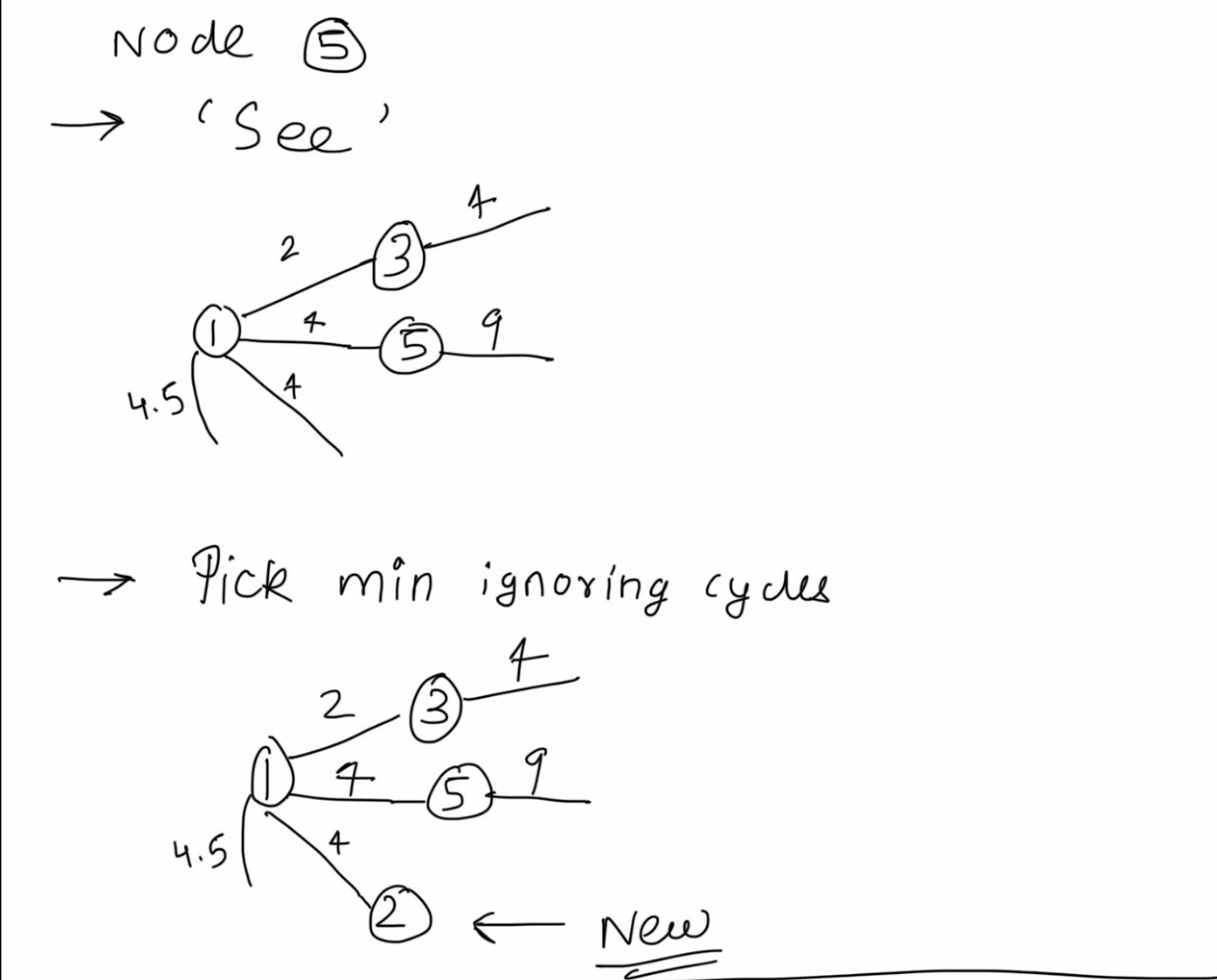
Repeat with me: see, pick and ignore. Note that ignore is conditional - only if cycles are formed. We will soon see an example.
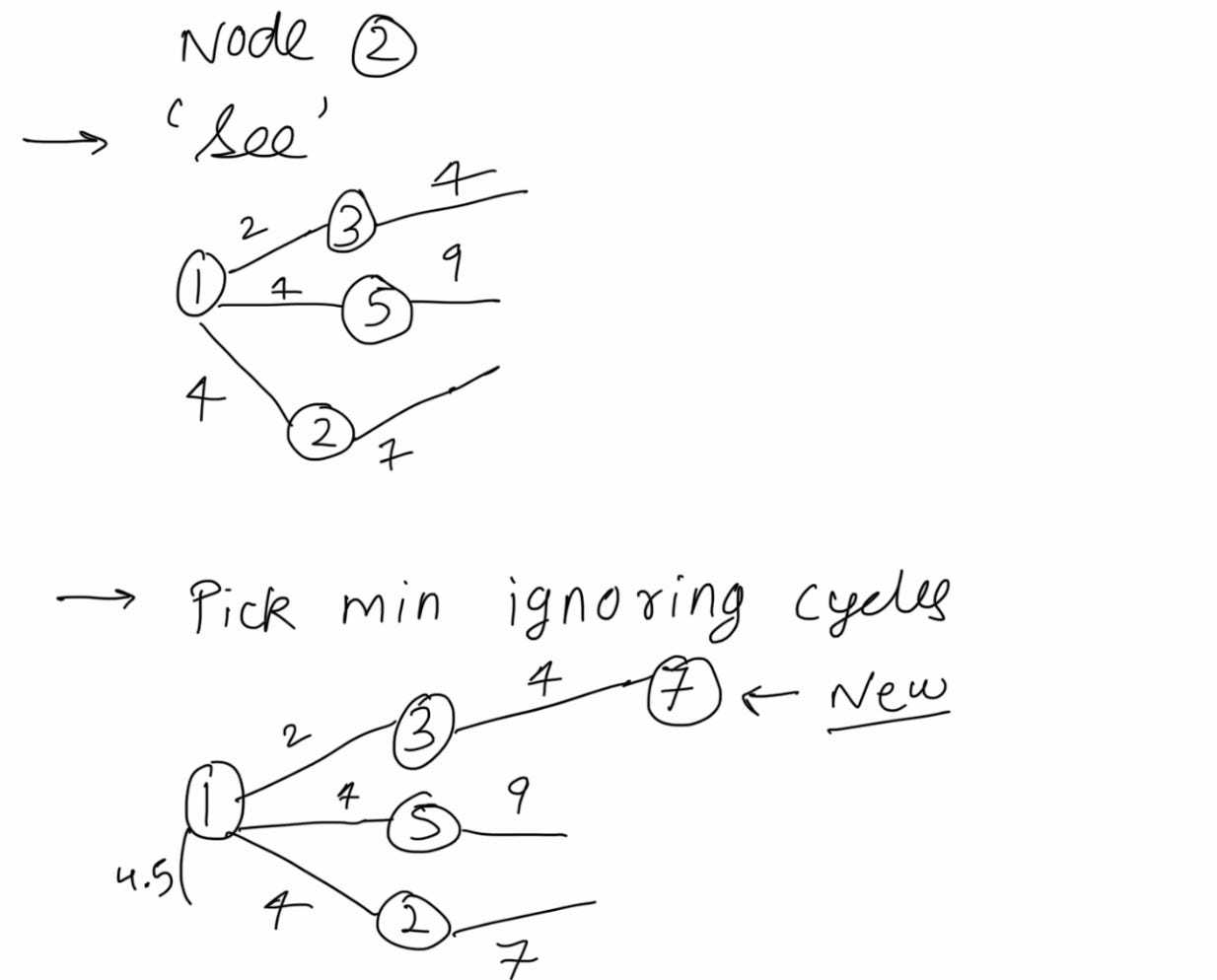
Another serving of see, pick and ignore
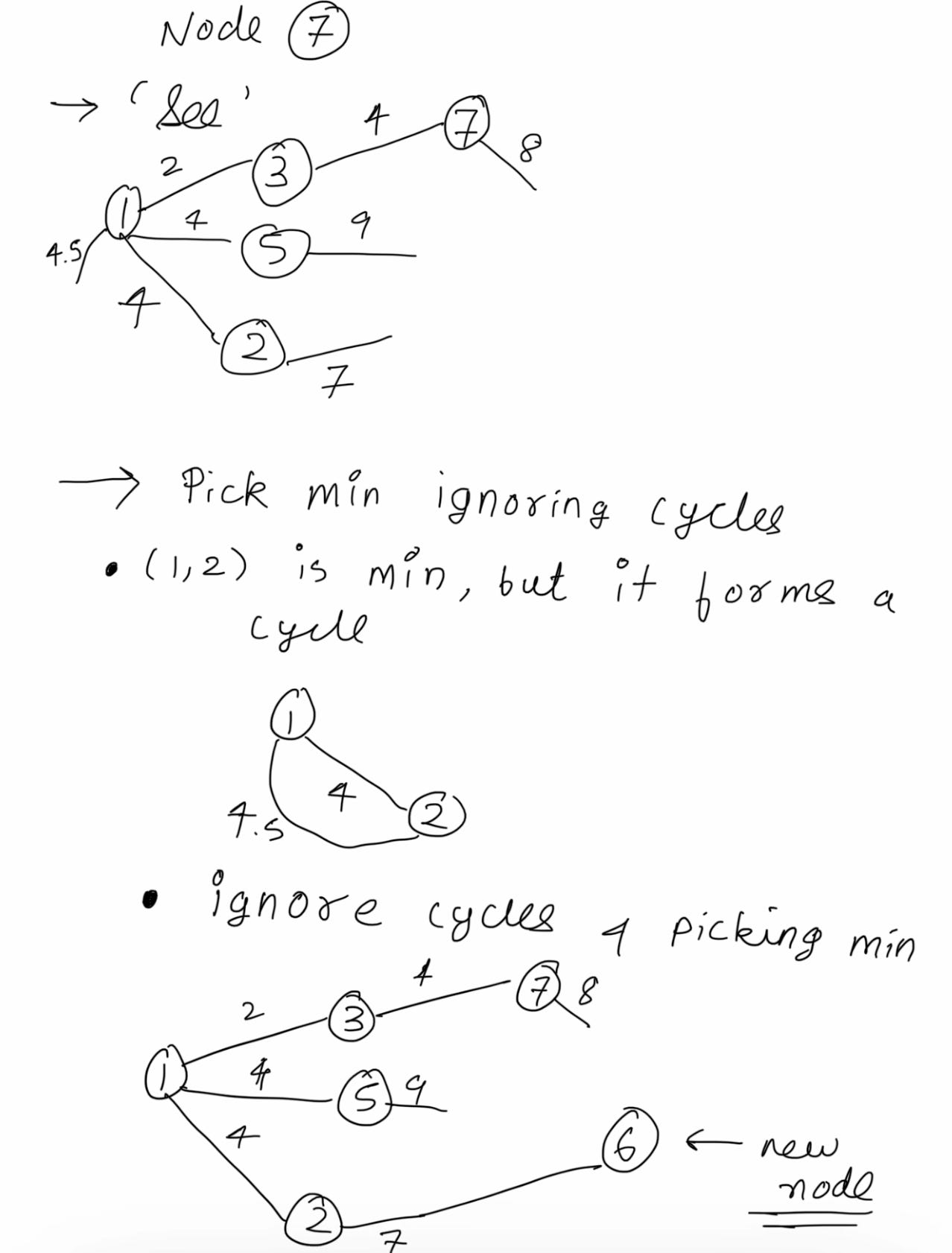
Some fresh see, pick and ignore, but this time you actually get to ignore.
And we are done!
Skeleton
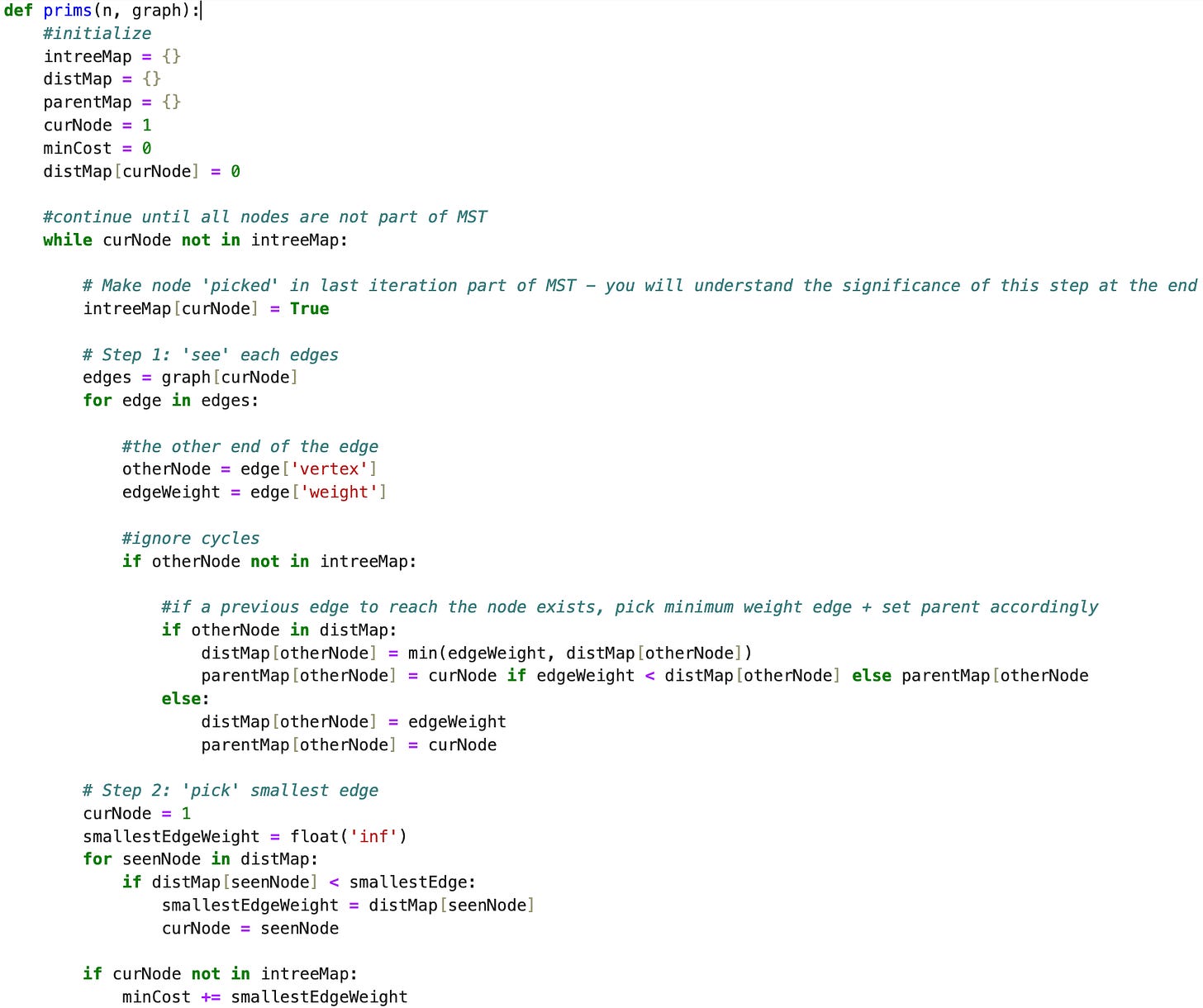
Here’s how you would implement Prim’s to construct MST for a real graph:
Correction: In the ‘Step 2’ for loop, you will also check if seenNode is not in intreeMap:
if distMap[seenNode] < smallestEdge and seenNode not in intreeMap:
Dry Run
Ok, slightly intimidating I admit. Maybe a dry run would help?
Let’s run through one iteration of our code for this graph:
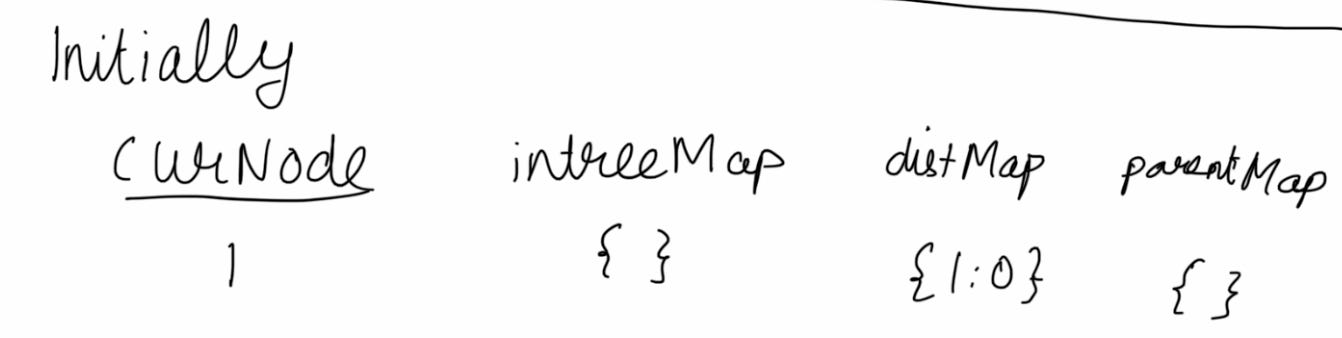
Initialize:
Enter the loop:
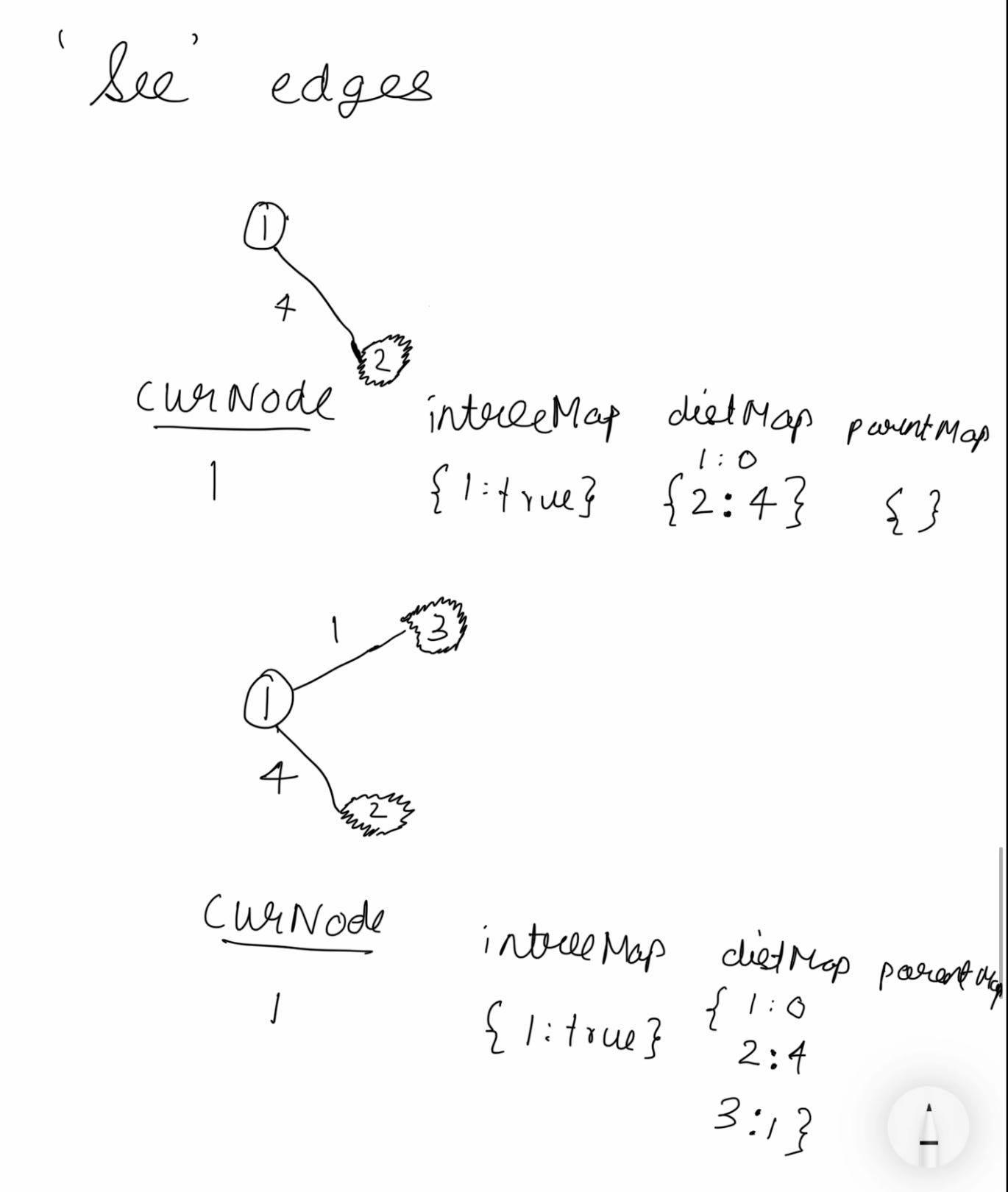
‘See’ edges, ignore cycles:
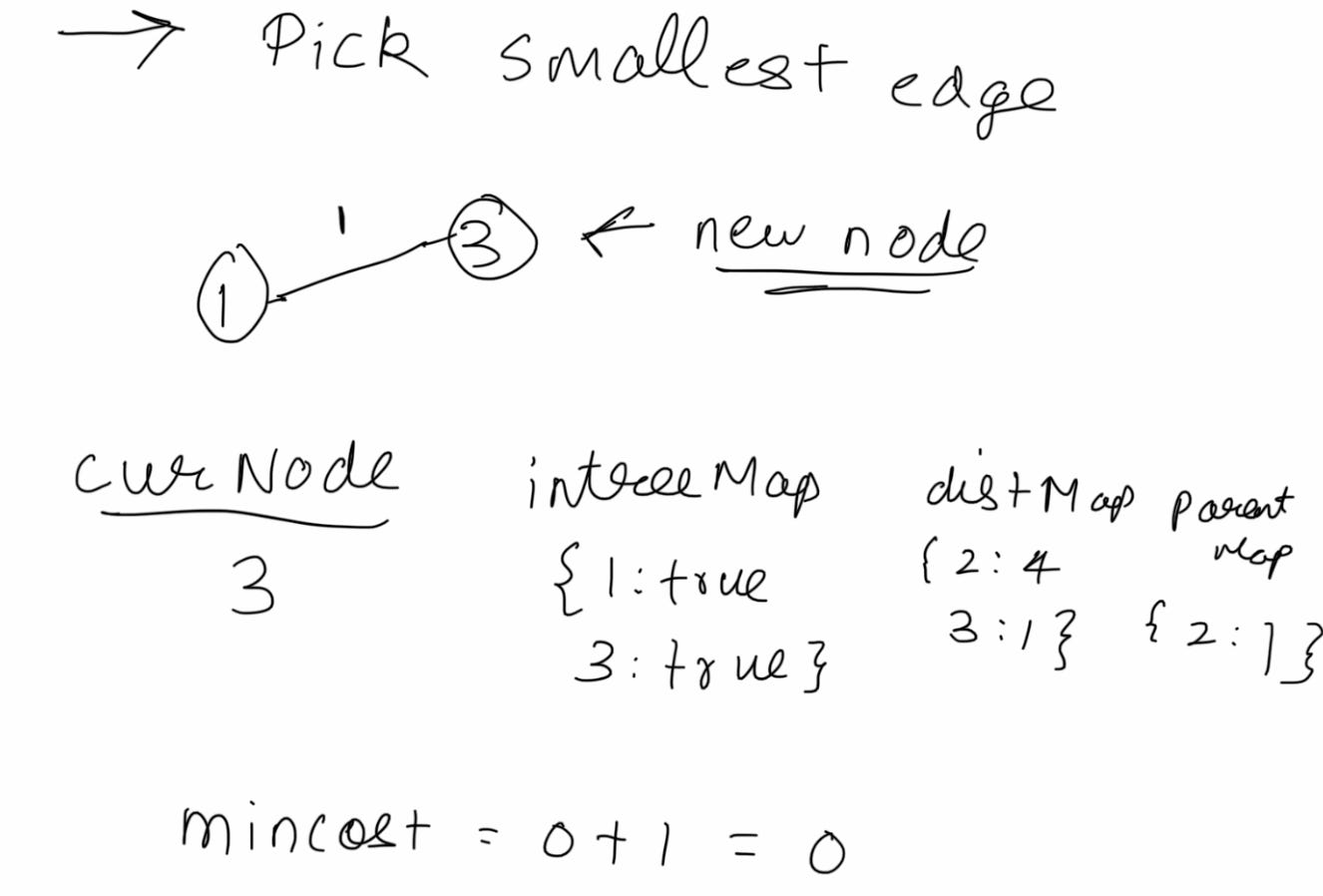
Pick smallest edge:
Solved Example
Solution for Min Cost To Connect All Points using Prim’s Algorithm
Note that our graph and edges will always be in a different form and we must be able to figure out how to extract them. Here we lean heavily on the ‘index’ of the point.
Things I skipped
Time and Space Complexity of the Algorithm: These things are usually implementation-dependent for Prim’s Algorithm. For the implementation above, the Time Complexity = O(Vertices ^ 2) and Space Complexity = O(Vertices). There are better implementations possible!
What to do next
Re-read the article until you feel you have a good grasp.
Solve Min Cost To Connect All Points by yourself.
Solve a very similar problem to solidify your understanding: Connecting Cities With Minimum Cost
If you are interested in MST’s, read up on Kruskal’s Algorithm or wait for my piece on it ;)
If you feel like you did not understand stuff, try following the other resources provided below. With a little effort, I am very sure they will be of help.